图的广度优先遍历算法-白红宇

前言

广度优先遍历算法是图的另一种基本遍历算法，其基本思想是尽最大程度辐射能够覆盖的节点，并对其进行访问。以迷宫为例，深度优先搜索更像是一个人在走迷宫，遇到没有走过就标记，遇到走过就退一步重新走；而广度优先搜索则可以想象成一组人一起朝不同的方向走迷宫，当出现新的未走过的路的时候，可以理解成一个人有分身术，继续从不同的方向走，，当相遇的时候则是合二为一（好吧，有点扯了）。

广度优先遍历算法的遍历过程

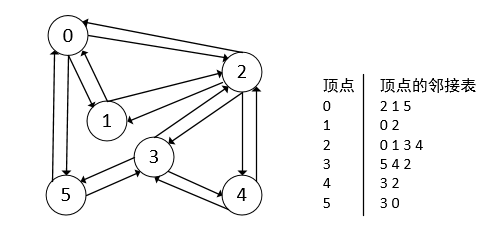
仍然以上一篇的例子进行说明，下面是广度优先遍历的具体过程：

从起点0开始遍历

从其邻接表得到所有的邻接节点，把这三个节点都进行标记，表示已经访问过了

从0的邻接表的第一个顶点2开始寻找新的叉路

查询顶点2的邻接表，并将其所有的邻接节点都标记为已访问

继续从顶点0的邻接表的第二个节点，也就是顶点1，遍历从顶点1开始

查询顶点1的邻接表的所有邻接节点，也就是顶点0和顶点2，发现这两个顶点都被访问过了，顶点1返回

从顶点0的下一个邻接节点，也就是顶点5，开始遍历

查询顶点5的邻接节点，发现其邻接节点3和0都被访问过了，顶点5返回

继续从2的下一个邻接节点3开始遍历

寻找顶点3的邻接节点，发现都被访问过了，顶点3返回

继续寻找顶点2的下一个邻接节点4，发现4的所有邻接节点都被访问过了，顶点4返回

顶点2的所有邻接节点都放过了，顶点2返回，遍历结束

广度优先遍历算法的实现

与深度优先遍历算法相同，都需要一个标记数组来记录一个节点是否被访问过，在深度优先遍历算法中，使用的是一个栈来实现的，但是广度优先因为需要记录与起点距离最短的节点，或者说能够用尽可能少的边连通的节点，距离短的优先遍历，距离远的后面再遍历，更像是队列。所以在广度优先遍历算法中，需要使用队列来实现这个过程。下面是具体的实现代码（已附详细注释）：

package com.rhwayfun.algorithm.graph;import java.util.LinkedList;import java.util.Queue;/** * 广度优先搜索 * Title:BreadFirstSearch
 * Description:
 * @author rhwayfun * @date Dec 23, 2015 4:43:41 PM * @version 1.0 */public class BreadFirstSearch {
         //创建一个标记数组    private boolean[] marked;    //起点    private int s;    public BreadFirstSearch(MyGraph G, int s){        marked = new boolean[G.V()];        this.s = s;        //开始广度优先搜索        bfs(G,s);    }    private void bfs(MyGraph G, int s2) {        //创建一个队列        Queue
     
       queue = new LinkedList
      
       ();        //标记起点        marked[s] = true;        queue.add(s);        System.out.print(s + " ");        while(!queue.isEmpty()){            //从队列中删除下一个节点            int v = queue.poll();            //将该节点的所有邻接节点加入队列中            for(int w : G.adj(v)){                //如果没有标记就标记                if(!marked[w]){                    marked[w] = true;                    System.out.print(w + " ");                    queue.add(w);                }            }        }    }}

运行该程序，发现广度优先遍历算法对上图的遍历顺序是0，2，1，5，3，4。